In 2022, state-of-the-art language models struggled with basic math word problems. Three years later, they're proving new theorems. In this post, we examine recent case studies where GPT-5 and similar systems have moved beyond solving textbook exercises to contributing genuine mathematical discoveries, from extending probability theory results to suggesting key ideas in quantum complexity proofs. Looks like LLMs have evolved from computational curiosities to “mediocre but not completely incompetent graduate students”. The implications for mathematical practice are profound: the bottleneck is shifting from having ideas to orchestrating, verifying, and formalizing them.
In 2022, “LLMs doing math” largely meant benchmark gains on datasets like MATH or GSM8K. No, scratch that. The MATH dataset actually contains quite complicated problems in natural language like the ones below (the illustration compares MATH problems with other similar datasets existing in 2021):
In 2022, these problems could be sometimes—quite rarely—solved by specially fine-tuned LLMs or mathematical systems with a separate theorem prover. Actual LLMs were far worse.
Remember the original chain-of-thought paper by Wei et al. (2022)? Their basic idea was to improve few-shot prompting (remember few-shot prompting, by the way? it was very important three years ago, and completely irrelevant a year after that) by providing examples with full solutions, not just the answers.
This core idea ultimately led to reasoning models, and it was a great idea, but I want to highlight a different thing. Here are the actual examples by Wei et al. (2022), the kind of problems where they got significant improvements thanks to chain-of-thought prompting:
These were frontier mathematical problems for (pure) LLMs in early 2022, three and a half years ago. Gives you some idea of the speed of progress, right?..
Two things have changed since then. First, large reasoning models learned to usefully spend additional compute on thinking, weaving together complicated reasoning. Second, LLM-based agents learned to successfully search for and themselves produce various artifacts such as preexisting research papers or code for validating or falsifying various hypotheses.
Both of these things were immediately useful for mathematics. As soon as OpenAI had their o` family of reasoning models, they both tested it on mathematical problems and provided access to real mathematicians. Famously, as early as September 2024 they asked Terence Tao—one of the best mathematicians in the world—to play with their just-appeared reasoning models, and he loved the o1 family: “The experience seemed roughly on par with trying to advise a mediocre, but not completely incompetent, (static simulation of a) graduate student”. I also recommend listening to this discussion with Tao and two leading OpenAI researchers.
On August 20, Sebastien Bubeck posted on X that GPT-5 is already capable of proving new theorems. Here is his report: “I took a convex optimization paper with a clean open problem in it and asked gpt-5-pro to work on it. It proved a better bound than what is in the paper, and I checked the proof it's correct”. The post went viral, and some of the results we discuss below were inspired by it.
Does it mean that grad students are already a species on the way to extinction, and the bell is tolling for grown-up mathematicians? Before trying to answer this question, let’s gather some more context first. What are the other recent successes of AI models in mathematics?
Before discussing what individual mathematicians can do with off-the-shelf LLMs, let's look at what happens when you build a more elaborate AI system specifically for mathematical discovery. AlphaEvolve, developed by DeepMind and announced in May 2025, represents a different paradigm: instead of a single LLM answering prompts, multiple LLMs work together in a loop of proposal, criticism, and empirical testing.
The core architecture extends earlier systems like FunSearch (which discovered new constructions in combinatorics) and AlphaTensor (which found faster matrix multiplication algorithms). In AlphaEvolve, several LLM instances play different roles: some propose candidate solutions, others critique them, and verification systems test whether the proposals actually work. The system operates in domains ranging from scheduling algorithms to combinatorial geometry, essentially anywhere you can quickly verify whether a proposed solution is correct.
What makes AlphaEvolve particularly interesting is that it doesn't just optimize within known solution spaces—it can discover genuinely novel constructions. The LLMs propose new mathematical objects (graphs, formulas, algorithms), other LLMs analyze their properties and suggest improvements, and the cycle continues until something better than existing results emerges.
But that’s old news. The recent work I want to highlight here is from late September. Nagda et al. (DeepMind, Sep 30, 2025) reported using AlphaEvolve to advance several open problems in theoretical computer science. Their most striking result came in the MAX-4-CUT problem, which asks: given a graph, how well can you partition its vertices into four sets to maximize edges crossing between different sets? This is a fundamental optimization problem with applications in VLSI design and clustering.
Previous work had established that MAX-4-CUT cannot be approximated better than a factor of 0.9883 unless P=NP (a "hardness of approximation" result). The proof of such results typically requires constructing a clever "gadget"—a small graph that, when used as a building block in a reduction, demonstrates the hardness. AlphaEvolve discovered a new 19-vertex gadget with a very unusual structure: highly asymmetric edge weights that previous human researchers hadn't considered.
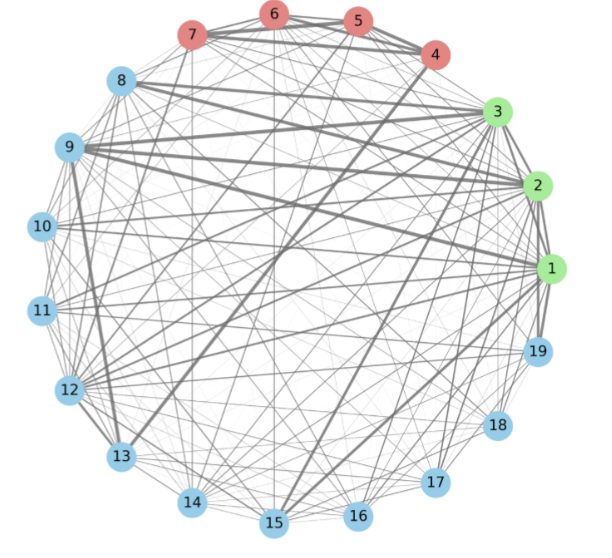
This gadget improved the hardness bound to 0.987, a genuine advance in our understanding of the problem's inherent difficulty.
In a separate result, AlphaEvolve found a new 4-regular Ramanujan graph with improved properties for 2-cut analysis. Ramanujan graphs are highly symmetric, optimally expanding graphs that arise in number theory, and finding explicit constructions with specific properties is notoriously difficult. The system's ability to navigate this space—proposing candidates, checking their spectral properties, and iterating—demonstrates a capability that goes beyond pattern matching in training data.
However, AlphaEvolve remains a research system, not a tool you can easily run yourself. Each successful run requires substantial computational resources and careful problem setup. The scaffolding—how to represent the problem, what tests to run, how to evaluate progress—still requires significant human expertise. As the DeepMind team emphasizes, AlphaEvolve works best as a "research partner" rather than an autonomous system.
This sets up an interesting contrast with the case studies we'll examine next. AlphaEvolve shows what's possible with heavy computational investment and specialized architecture. But can individual mathematicians, working with standard off-the-shelf LLMs and modest prompting, already get meaningful research assistance? Let's find out.
Inspired by Bubeck’s success in convex optimization that we discussed above, Diez et al. (September 3, 2025) tried to use GPT-5 for their own field of mathematics. Specifically, they considered the Malliavin–Stein method that is used in probability theory to study the speed of convergence towards normal distributions (much of probability theory stems from various involved analyses of the central limit theorem).
Specifically, their question was how fast certain random objects (so-called “Wiener chaoses”) converge to the normal distribution. I will not go into the mathematical details in a post like this one, intended for the general public, but the basic idea was this: they considered objects for which a qualitative result was already known, i.e., it was known that they converge to the normal distribution. The question was to obtain a quantitative result, i.e., estimate the rate of convergence.
They did not make it especially easy for GPT-5. Here is their full prompt for this experiment (I suppose the papers were attached, but maybe GPT-5 doesn’t even need that):
Looks more like a conjecture left open for future work than an in-depth talk with a graduate student that’s inevitable if you present her with a new problem.
From this prompt, GPT‑5 immediately produced the right shape of result and proof, but with a significant mistake in a covariance expansion. After two nudges (“can you check your formula…” and, failing that, a pointed correction), the model repaired its argument and delivered a clean statement.
After this brief interaction, all that remained was to ask GPT to write the paper:
Moreover, the authors asked GPT-5 to produce a “Concluding Remarks” section with possible extensions and future work. The model suggested an extension from the Gaussian to the Poisson case, which is a very natural idea in this context, and the authors tried to take it up on the promise.
In a fresh session, GPT‑5 correctly noticed the differences between the Gaussian and Poisson cases, but again made an oversight: it missed an important fact that was present in the original paper this inquiry had started from. When the fact was pointed out, GPT-5 correctly proved a new theorem for the Poisson case.
So Diez et al. successfully made GPT-5 prove two new theorems, albeit quite straightforward ones (application of a known general technique to a novel case) and with mistakes that were successfully corrected but first had to be pointed out to the model. What was their conclusion about this process?
To be honest, this sounds somewhat defensive. Of course the first steps of LLMs proving novel theorems should look exactly like this—that's what “first steps” means. And the rate of progress suggests these first steps will quickly be followed by second, third, and beyond.
And you know what’s the cherry on top here? If you look at the Appendix of Diez et al. (2025), where they show their interactions with GPT-5, you can notice that they did not even use GPT-5 Pro!.. The thinking times of 2-3 minutes are characteristic of the standard GPT-5-Thinking model, I cannot imagine GPT-5 Pro spending so little time to try and prove a novel theorem. So the authors’ conclusions were not even about the best model in the one standard off-the-shelf family (Gemini is not bad at math either!) they tried…
Taking this further, Feldman and Karbasi (Sep 22, 2025) proposed the Gödel Test: can a large language model prove correct solutions to very simple but genuinely new conjectures? Not Olympiad problems from a public archive (or even new but still designed with solutions in mind) but easy, fresh lemmas that do not already exist on the web or in textbooks.
To make the test concrete (and fair), they stayed inside a well-scoped slice of theoretical CS and optimization: submodular maximization and its continuous counterparts. This field has a rich toolkit, including greedy, continuous greedy, and the Frank-Wolfe algorithm, matroid constraints, and a rich field of their relaxations, and clear baselines for what a “routine” proof looks like.
Even more specifically, they concentrate on submodularity. It is the “diminishing returns” property: if you're selecting photos to represent a vacation, the tenth photo adds less value than the first one. This property appears everywhere in machine learning: in feature selection, data summarization, influence maximization and more, and in continuous form (DR-submodularity) it connects to projection‑free optimization over polytopes. In other words, submodularity-related problems present a sweet spot where a competent grad student can stitch together standard templates to settle simple conjectures.
Feldman and Karbasi designed five conjectures at the boundary of what a strong undergraduate or early graduate student might solve in a day. For each, they gave GPT-5 minimal context—a short prompt and one or two reference papers (not their own work)—then asked for a complete proof, sometimes in LaTeX. No interactive hints. No iterative refinement. Just: here's the problem, here's some background, prove it.
Let us walk through the first two conjectures as examples. Continuous (DR-)submodular maximization under convex constraints is a workhorse abstraction for ML objectives where gradients exhibit diminishing returns. Projection‑free methods (Frank-Wolfe and continuous greedy variants) work well when the feasible region is a huge polytope with a cheap linear optimization oracle. The optimization problem here is to maximize F=G+H where G is nonnegative monotone DR‑submodular and H is nonnegative DR‑submodular (not necessarily monotone) over a down‑closed polytope P. The authors asked GPT‑5 to adapt the preexisting Measured Greedy Frank-Wolfe analysis to produce a split guarantee F(x)≥αG(o)+βH(o)−err with α, β as constants and an ϵ-vanishing error:
The result? GPT‑5 recovered essentially the right template and delivered the expected constants (informally, α≈1−1/e, β≈1/e in the non‑monotone case), with a few loose ends (mask bounds, a missing monotonicity flag in one inequality) and a tendency to follow the source proof “too closely”. The authors call this the “lazy but adequate” adaptation: correct in spirit, thin on intermediate steps, and sticking to the original skeleton even when a cleaner specialization would do.
For the second conjecture, the authors considered bicriteria maximization. Bicriteria algorithms intentionally relax feasibility (e.g., allow the solution to be a union of a few feasible sets) to approach 1−ε value, which is useful when the exact constraint is too tight for near‑optimal value. These algorithms were well studied for matroid constraints, and Feldman and Karbasi asked to extend the analysis to a different type of constraints known as p-systems:
The results were even more interesting: GPT‑5 proposed a multi‑pass greedy algorithm that provided a different guarantee than the authors suggested, refuting their conjecture (talk about sycophancy!) and yielding a more sensible dependence on p. The proof was not without minor problems, but generally it held up to scrutiny. This is still very far from a Fields Medal, but it’s above rote regurgitation.
Not every test was a success, but on three of five tasks, the model correctly adapted known proof patterns with modest fixes. That’s far from trivial: reading a paper, pulling out the operative inequality, and inserting the right constants is a real skill, previously out of reach for LLMs.
Note that in this test, the setting was harder for LLMs. The Mallavin-Stein experiment showed that guided models can now help push known techniques to new instances. The Gödel Test suggests that even in unguided mode they often behave like an earnest junior collaborator: good at reading, decent at adapting, sometimes insightful, but still unable to truly verify its own work and often too confident when wrong. Again, this is exactly the kind of incremental step you’d expect on the way from “LLMs can simulate worked examples” to “LLMs can genuinely contribute to new mathematics”.
And again: this was not even GPT-5 Pro! This time, the paper clearly states that it was GPT-5-Thinking.
quantum complexity theory and for making the field legible to a broad audience (Complexity Zoo, the book Quantum Computing Since Democritus, and the long‑running blog Shtetl‑Optimized). He’s the Schlumberger Centennial Chair in CS at UT Austin and directs its Quantum Information Center.
In 2022–2023 he also worked at OpenAI on theoretical directions in AI safety (famously blogging about it: “OpenAI!”). That work is part of why Scott Aaronson is so deeply attuned to the recent developments in LLMs, and also why his recent post about GPT‑5 helping with a quantum‑complexity proof, titled “The QMA Singularity”, drew so much attention across both TCS and AI circles. Unlike some deep and involved mathematics, in this case I think we do have a chance to actually understand what is going on there, so let me elaborate. Readers already familiar with complexity theory can skip ahead.
In theoretical computer science, a complexity class is just a bucket of decision problems grouped by the resources a model of computation needs to solve them: time, space, randomness, quantum amplitudes, interaction, and so on. The usual baseline classes are:
To get to QMA, first we need to make a leap from proofs you read to proofs you interact with. In an interactive proof, the verifier (limited to polynomial time) and an all‑powerful prover (oracle that knows everything and can compute everything) exchange messages. The verifier uses randomness, and the prover can try to cheat, but two guarantees must hold:
Here’s an illustration by Alp Bassa:
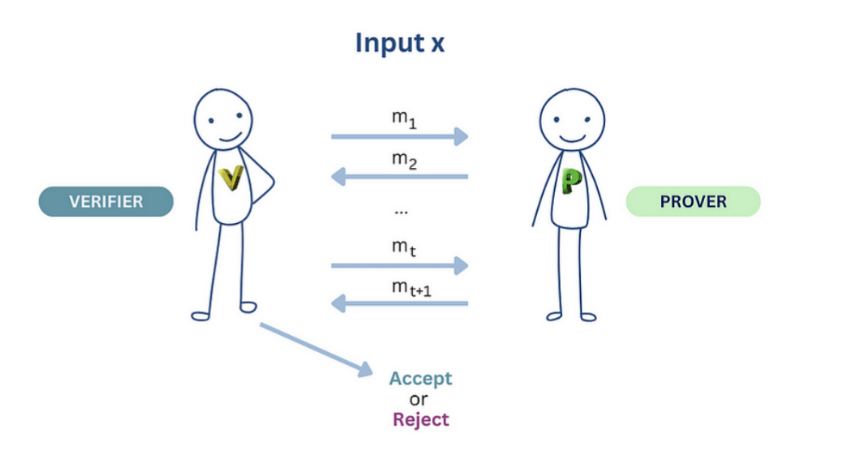
The Arthur–Merlin model is the public‑coin version of interactive proofs: Arthur (the verifier) flips random coins in public, Merlin (the prover) replies, and then Arthur decides.
One round of “Merlin then Arthur” is called the MA class (think NP but Arthur may randomize when checking); two rounds (first Arthur’s public coins, then Merlin’s message) give the AM complexity class. Results like IP = PSPACE and relations among MA/AM fit into the classic diagram of interactive‑proof classes. For a concise reference and terminology, see the Wikipedia entries on Arthur-Merlin and interactive proofs.
Many of these classes have quantum counterparts; for example, BQP is the quantum analogue of BPP, that is, a problem is in BQP if there exists a quantum algorithm that solves it with high probability and is guaranteed to run in polynomial time. The famous Shor’s algorithm for integer factorization basically says that factorization is in BQP, while it is not known to be in BPP.
Think of QMA (Quantum Merlin-Arthur) as the quantum analogue of NP: Merlin sends Arthur a quantum state as a witness, Arthur runs a polynomial-time quantum verification algorithm, and accepts or rejects. The quantum twist is that Arthur's verification can exploit superposition and entanglement. Again, two properties matter: completeness (accept a valid witness with high probability) and soundness (reject all invalid witnesses with high probability).
As in classical complexity, we can “amplify” a small gap to a larger one by repeating and post‑processing. But a long‑standing problem has been whether we can make completeness perfect, i.e., whether we can always accept correct witnesses; this is known as the QMA =/≠ QMA₁ problem, 1 being the probability. In 2008, the same Scott Aaronson showed a quantum‑oracle separation: QMA ≠ QMA₁ if the algorithms involved are given access to a certain oracle. This sounds like a very technical contribution but what it actually means is that any proof that will collapse QMA = QMA₁ must use ideas that do not relativize, i.e., do not survive adding an oracle. This rules out large classes of standard complexity theory approaches.
In June 2025, Jeffery and Witteveen gave a black‑box amplification that pushes QMA completeness error to doubly‑exponentially small, that is, ≈ 1/exp(exp(n)); simply repeating the algorithm and taking majority will give you only a single exponent. Finally, in late September Aaronson and Witteveen proved that this is optimal for any black‑box approach: you can’t push completeness closer to 1 than the double exponent (nor soundness below exponentially small) by black‑box means.
The surprise, and the reason this story went viral, is how the authors arrived at a key step in that optimality proof: GPT‑5‑Thinking suggested the right analytic “observable” (a mathematical quantity to track) after a few minutes of back‑and‑forth, much like brainstorming with a junior collaborator. Aaronson called this the “QMA Singularity”. Here is his account of this interaction:
This is a great account of how actual mathematical work can go with the help of LLMs. GPT-5 did not give (or even try to give) a formal IMO‑style prompt. The researchers had already set up the oracle separation framework and were stuck on how to certify that the top eigenvalue can’t stay too close to 1 for too long in θ, given degree constraints. They asked GPT‑5‑Thinking for a way to “encode” the closeness of λmax to 1 into a rational function of controllable degree. The model did not brute‑force a formal proof; rather, it inserted a key idea that unlocked the proof for humans who already knew the terrain.
There is an amusing coda to this: a commenter later proposed an even simpler function, det(I-E), which the authors think also works and streamlines an open sub‑question; it was written into the second version of the paper. Scott quipped that it was “human supremacy restored, for now”... though of course the original LLM contribution remains central to the proof's existence.
Taken together, these case studies point to a clear if uncomfortable update: frontier LLMs can now meaningfully contribute to research mathematics. Perhaps not at the Fields Medal level yet, but at the “one conceptual step from existing literature” level that represents the majority of published mathematics.
Pattern 1: Extension-by-technique is within reach. In the Malliavin-Stein experiment, GPT‑5 converted a qualitative convergence statement into a quantitative one and then carried the idea across from the Gaussian to the Poisson setting. It made a blunder (twice) on a covariance expansion and missed a key positivity fact in the Poisson case until nudged—but with a couple of pointed corrections, it delivered a clean theorem and counterexample. That is exactly the profile of “apprentice research”: knows the toolbox, sometimes stumbles on relatively simple steps, but adapts when corrected.
Pattern 2: Minimal prompting can still surface new, correct content. In the Gödel Test, the setup withheld the authors’ conjectures and provided only one or two source papers per problem. On three of five submodular‑optimization conjectures, the model produced nearly correct solutions; on one, it even refuted the authors’ original claim by deriving a different approximation guarantee that stood up to checking. Failures were observed where cross‑paper synthesis was needed or when an analysis was more delicate than the algorithmic idea. That’s a useful boundary condition for where human glue is still essential.
Pattern 3: LLMs can now propose genuinely new ideas. In quantum complexity, Aaronson & Witteveen quantify an amplification barrier for QMA and explicitly note that the rational‑function trick they use (trace of (I−P(z))−1 to control how close completeness can get to 1 under black‑box amplification) was suggested by GPT‑5‑Thinking. The result itself is incremental, but the workflow is the breakthrough: the model provided the right analytic lens, a seed that humans then turned into a full proof.
Scott Aaronson’s phrase “obvious with hindsight” captures the current frontier very well. The current LLMs won't yet pull revolutionary insights from thin air. But they excel at the combinatorial middle ground: taking technique A from paper X and method B from paper Y, recognizing they could work together, and handling the (still non-trivial) details of making them fit. This is precisely the skill that separates productive researchers from those who struggle, and it's no longer uniquely human.
Viewed against the backdrop of 2022–2025, this is a steep curve. In early 2022, “LLMs doing math” meant chain‑of‑thought tutoring for contest‑style problems. By late 2025, we have off‑the‑shelf reasoning models that can (a) push a known technique into a fresh quantitative regime, (b) handle easy but new conjectures with little hand‑holding, and (c) occasionally contribute the key move in a research‑level proof.
What comes next? Several trends seem clear:
As in software development, the human role moves from pure creation to orchestration: problem framing, idea triage, verification, and proof engineering. In this future, human mathematicians remain central—but the mix of tasks, and the speed at which we cycle through them, changes fast. Whether this is something to celebrate or worry about, I'll leave to you.
DeepMind has introduced an AI system that behaves like a tireless research assistant- reading papers, rewriting code, and systematically improving scientific methods. By combining a code-rewriting LLM with intelligent tree search, it automates the tedious parts of experimentation. This marks a major step toward the “AI co-scientist,” accelerating discoveries across fields from genomics to forecasting.
Read post
Meta FAIR’s new Vision Language World Models (VLWM) take a fresh approach to AI planning: instead of predicting pixels or manipulating abstract vectors, they describe future states and actions in plain English. This makes plans interpretable, editable, and easier to trust, bridging the gap between perception and action. VLWM uses a pipeline of video-to-text compression (Tree of Captions), iterative refinement, and a critic model to evaluate alternative futures, achieving state-of-the-art results in visual planning benchmarks. While challenges remain—like text fidelity, dataset quality, and limits on fine-grained control—VLWM marks a major step toward human-AI collaborative planning.
Read post
Apolo turns your Data Center into an AI Powerhouse.
.svg)
.svg)
© 2025 Apolo Cloud Inc. All rights reserved.
