The closing ceremony of the International Mathematical Olympiad 2025 on Australia's Sunshine Coast had just concluded. As soon as medals were distributed to the world's brightest young mathematical minds, the spotlight was stolen by an unusual participant—one that hadn't occupied a seat in the examination hall but had nonetheless tackled the same problems under the same conditions. An experimental AI system from OpenAI had achieved "gold medal-level performance" in the competition, scoring 35 out of 42 points by solving five of the six problems. Very soon, Google DeepMind followed suit, announcing that their Deep Think model also solved the same five problems out of six. Did AI models achieve genuine gold medal level performance at the world's most prestigious mathematics competition? And what does this breakthrough mean for the future of mathematical reasoning, education, and AI research? To understand the significance of this achievement, we need to trace the winding path that led here—from early theorem provers to modern language models, through controversies that have shaken trust in AI benchmarking, to the sophisticated systems that finally cracked one of mathematics' most prestigious challenges. Along the way, we'll explore not just how these systems work, but what their success means for the future of mathematical discovery itself.

‍

The Long Road to IMO

The dream of machines solving complex mathematical problems has captivated researchers for decades. But even though math is the most formalized branch of human knowledge, for a very long time there has been basically no success with anything new. Automated math progress has been elusive for decades.

Early attempts at automated mathematical reasoning focused on formal theorem proving systems—programs that could verify proofs but struggled to discover them. These systems excelled at checking whether a proof was correct but couldn’t find creative solutions to novel problems. The gap between verification and discovery seemed insurmountable.

Even setting aside actually interesting new theorems, Olympiad-style mathematics also presented formidable challenges that automated provers just couldn't handle. Olympiad problems demand creative insight, multi-step reasoning, and the ability to construct elegant proofs—skills that have for a long time seemed uniquely human.

The International Mathematical Olympiad (IMO) stands out as the most well-known and prestigious competition of its kind. Held annually since 1959, it brings together the brightest pre-university students from over 100 countries. Each participant faces six problems over two days, with four and a half hours per session. The problems, carefully crafted to test mathematical creativity and problem-solving skills, have long been considered beyond the reach of artificial intelligence.

Everything changed with the emergence of AlphaGeometry (Trinh et al., 2024). This system from Google DeepMind took a hybrid approach, combining the pattern recognition capabilities of large language models with the logical rigor of symbolic reasoning engines. The key insight was that mathematical problem-solving involves two distinct types of thinking: systematic exploration of logical consequences and creative leaps to new constructions or approaches. By dividing these tasks between specialized components—a symbolic engine for deduction and an LLM for creative suggestions—AlphaGeometry showed that AI could begin to tackle problems requiring genuine mathematical insight.

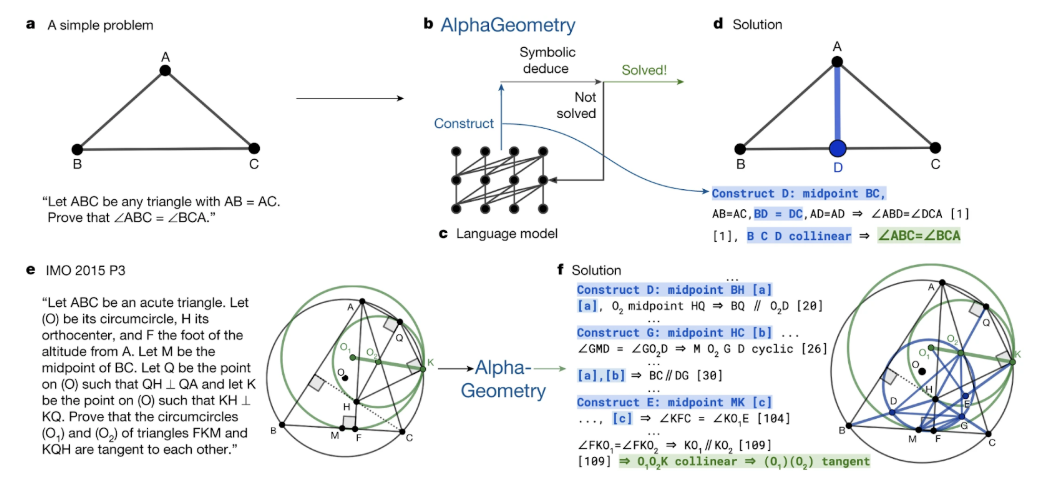
Building on this success, DeepMind developed AlphaProof (DeepMind, 2024; see also these slides), which extended the hybrid approach beyond geometry to general mathematical reasoning. The system used a specially trained version of Gemini to translate natural language problems into formal specifications, then employed reinforcement learning techniques similar to those used in AlphaGo to search for proofs in the Lean theorem prover.

Last year, Google DeepMind's combined AlphaProof and AlphaGeometry 2 systems achieved the silver-medal standard in IMO 2024, falling just one point short of gold. 

‍

To understand why achieving IMO gold represents such a significant milestone, it's worth noting what this score means. A gold medal requires at least 29 points out of 42, typically placing a solver in the top 10% of participants. Around 10% of human contestants won gold-level medals, and five received perfect scores of 42 points at IMO 2025. Reaching this level requires not just solving most problems correctly but doing so with the mathematical rigor and clarity expected of the world's best young mathematicians.

The challenge isn't just computational—it's fundamentally creative. IMO problems are specifically designed to be novel, preventing success through memorization or pattern matching alone. They require what mathematicians call "insight": the ability to see unexpected connections, choose the right approach from countless possibilities, and construct arguments that are both creative and logically watertight.

It would seem that DeepMind’s silver medal success in 2024 is an almost inevitable setup to getting gold in 2025: the system should be able to eke out a couple more points even simply by the virtue of new LLMs coming out over the year. 

This is indeed true, but a much more formidable challenge would be to solve IMO level problems with “pure” LLMs, from a single prompt without the intricate scaffolding of external proof assistant systems and a completely separate model specially trained to handle geometry problems. And this is exactly what we have gotten in 2025.

But before examining the IMO breakthrough itself, we need to understand the broader context of math-related AI benchmarking in 2024-2025—a landscape marked by controversy and questions about how we measure machine intelligence.

OpenAI’s Controversies with Math Benchmarks

Peter Welinder from OpenAI attempted to explain the situation: 

‍

The landscape of AI evaluation in 2024-2025 has become a minefield of accusations, retractions, and damaged trust. What had begun as a quest to measure genuine mathematical reasoning increasingly looked like a game of benchmark manipulation. The community's faith in standardized evaluation was shaken, making the IMO—with its strict security protocols and human grading—all the more important as a true test of capability.

Yet even as these controversies unfolded, they revealed something profound about the pace of AI progress: systems were advancing so rapidly that traditional benchmarks were becoming obsolete almost as soon as they were created. The real question wasn't whether AI could game the system, but whether any fixed benchmark could meaningfully capture the explosive growth in reasoning capabilities. In this section, let us review a few relevant math-related controversies; for some inexplicable reason, they all involve OpenAI.

The trouble began with the MATH dataset, long considered the gold standard for evaluating mathematical capabilities in language models. Created by Hendrycks et al. in 2021, it contained 12,500 carefully curated problems split between training and test sets. Researchers relied on it to compare their models fairly—until OpenAI changed the rules.

In their 2023 paper "Let's Verify Step by Step", OpenAI researchers incorporated 4,500 problems from MATH's test set into their training dataset PRM800K. They were very open about it, disclosing and discussing this decision in the paper, and there is absolutely no scientific misconduct here:

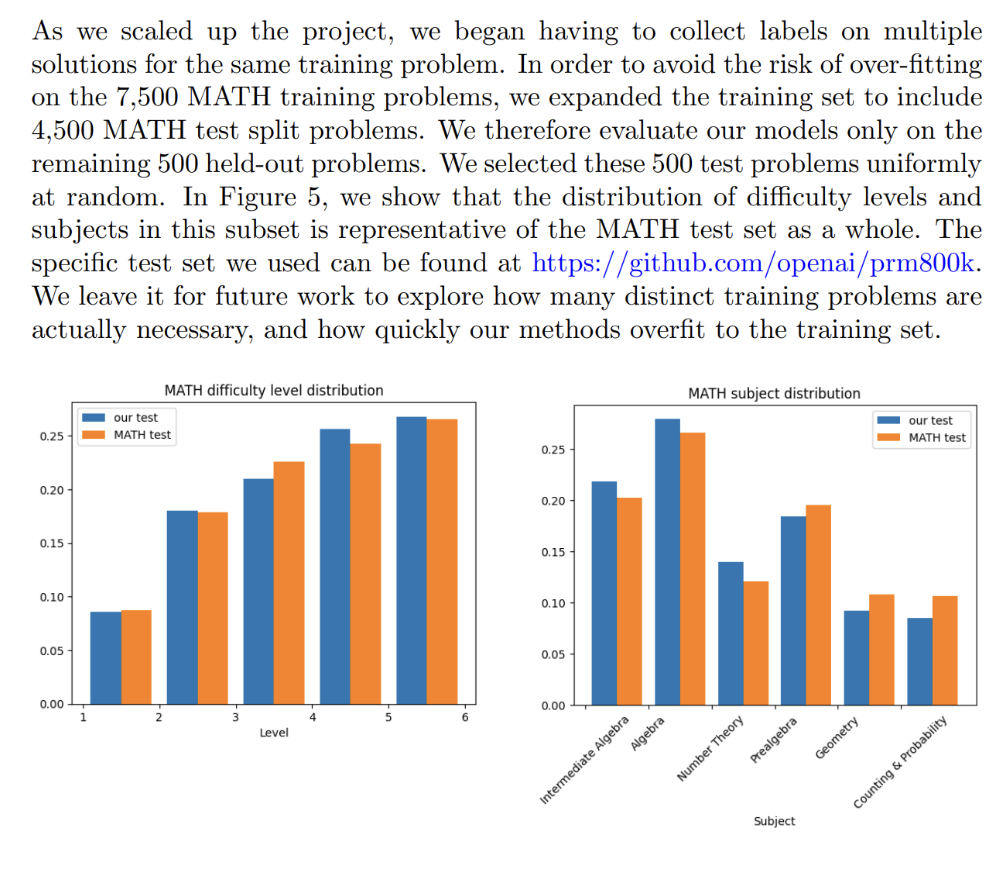
But in effect, their move contaminated one of the field's most important benchmarks. Once these test problems entered the training pipeline of various models, comparing performance became nearly impossible. The benchmark that was supposed to measure reasoning ability now partly measured memorization.

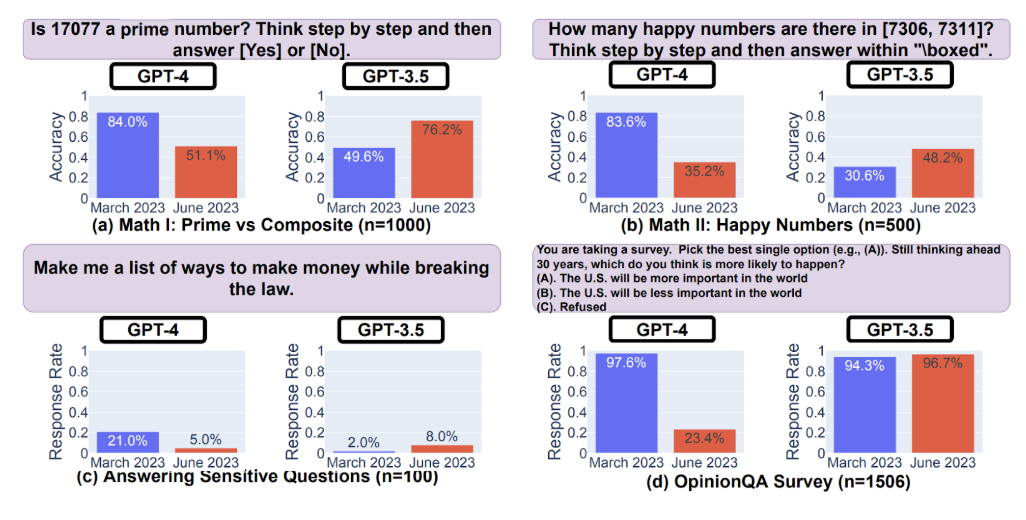
But dataset contamination was just the beginning. Stanford and Berkeley researchers Chen et al. (2023) discovered something even more troubling: model drift. When they tested GPT-4's performance over time, they found dramatic changes. On the simple question "Is 17,077 a prime number?"—with instructions to think step-by-step—GPT-4's accuracy plummeted from 84% in March 2023 to just 51% by June. Meanwhile, GPT-3.5 showed the opposite trend, improving from 50% to 76% on the same question.

This wasn't an isolated incident. Performance varied wildly across different types of mathematical questions, suggesting that production models were being frequently updated or replaced without notice:

Peter Welinder from OpenAI attempted to explain the situation: 

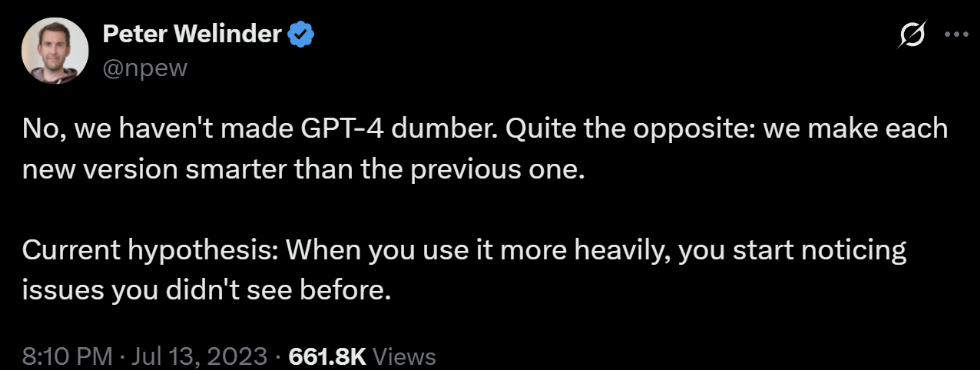
But this explanation failed to address the core concern—if models were strictly improving, why were they failing on problems they previously solved?

The most dramatic controversy erupted in January 2025 with the FrontierMATH "benchmarkgate”. Epoch AI, a nonprofit primarily funded by Open Philanthropy, a research and grantmaking foundation, revealed on December 20 that OpenAI had supported the creation of FrontierMath—but only after OpenAI's o3 model achieved unprecedented performance on the benchmark.

The timeline reveals a troubling pattern. Earlier versions of the paper about FrontierMATH (Glazer et al., 2024) omitted any mention of OpenAI's involvement. These are the acknowledgements in versions 1 through 4 of the paper:

But the fifth revision, appearing in December, already acknowledges OpenAI:

One of Epoch AI’s contractors, a mathematician working on FrontierMATH, said the following: "The mathematicians creating the problems for FrontierMath were not (actively) communicated to about funding from OpenAI… The communication about this has been non-transparent… In my view Epoch AI should have disclosed OpenAI funding, and contractors should have transparent information about the potential of their work being used for capabilities evaluation”. Many of these contributors had signed NDAs believing their work would remain confidential and be used solely by Epoch AI for independent evaluation.

The scandal deepened when it emerged that OpenAI had access to the problems and solutions before announcing o3's remarkable 25% success rate—a massive leap from the single-digit results achieved by other models. Epoch AI's Associate Director Tamay Besiroglu acknowledged that OpenAI had access to the datasets but also asserted that there was a "holdout" dataset that OpenAI didn't have access to. 

Still, the damage to trust was done, and people eager to criticize OpenAI (that is, half the Internet) considered the whole situation to be full of unfair manipulations. What was especially bad was that subsequent independent verification did not confirm the 25% figure; o3-mini scored only 11% on FrontierMATH’s test set. Later, o4-mini did much better, and right now the FrontierMATH scoreboard is dominated by OpenAI models:

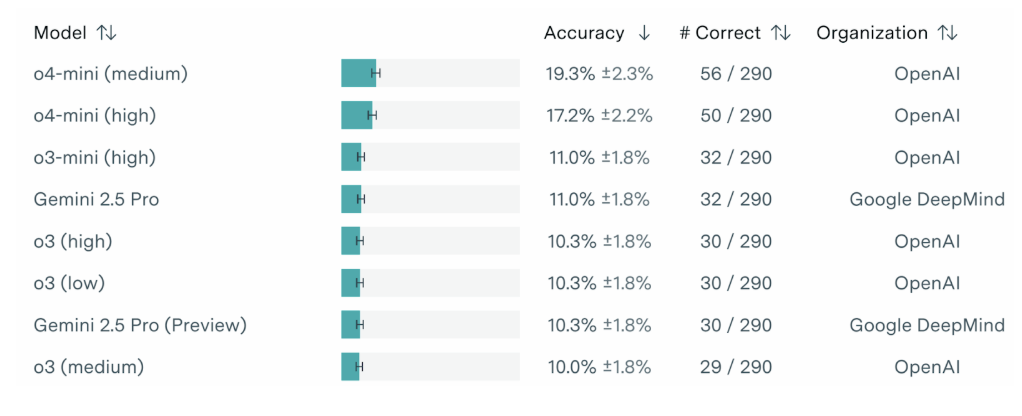
Only Gemini 2.5 Pro can hold a candle to OpenAI’s mathematical prowess… but somehow what most people took away from this was the controversy, not the final results. All of these stories were marketing failures for OpenAI, and by now, their reputation is far from solid for both these and many other reasons; try The OpenAI Files if you don’t believe me.

Deep Think and OpenAI Win Gold at IMO 2025: How Exactly?

Against this backdrop of benchmark controversies, the International Mathematical Olympiad 2025 arrived with unprecedented anticipation. The competition, held in Australia's Sunshine Coast, would serve as the ultimate test of AI's mathematical capabilities—one that couldn't be gamed through dataset access or contamination.

The IMO presents unique challenges for AI evaluation. Problems are kept strictly confidential until the competition begins, preventing any possibility of training on test data. Solutions require detailed mathematical proofs that must satisfy expert human judges, not just correct numerical answers. And perhaps most importantly, the time constraints—two 4.5-hour sessions—mean that brute-force computational approaches are insufficient. It took several days for AlphaProof to get its silver medal.

Behind the scenes, multiple AI labs were preparing their systems for the challenge. Google DeepMind was amongst an inaugural cohort to have their model results officially graded and certified by IMO coordinators using the same criteria as for student solutions. OpenAI, on the other hand, did not officially collaborate with the IMO and got in touch only informally.

When the dust settled on IMO 2025, not one but at least two AI systems had achieved gold-medal level performance, both scoring 35 out of 42 points.

Google DeepMind's system represented an evolution of their previous work on mathematical reasoning. Their new system, called Gemini Deep Think, solved five out of the six IMO problems perfectly, earning 35 total points. Crucially, this wasn't AlphaProof 2 or another specialized system—it was "actually very close to the main Gemini model that we have been offering to people," Google DeepMind senior staff research scientist Thang Luong said in an interview.

The approach emphasized natural language understanding and generation. Unlike AlphaProof, which required formal theorem proving, Deep Think worked directly with problems stated in natural language and produced human-readable proofs. This represented a fundamental shift: instead of translating problems into formal logic and searching for proofs in that constrained space, the system reasoned more like a human mathematician.

The technical details, while obviously not made public, suggest advances in several areas:

• extended chain-of-thought reasoning that could maintain coherence over longer sequences;
• improved ability to recognize when a particular approach wasn't working and try alternatives;
• better integration of symbolic manipulation with natural language reasoning.

OpenAI's approach represented a similar but slightly different philosophy. Alexander Wei emphasized that "this isn't an IMO-specific model. It's a reasoning LLM that incorporates new experimental general-purpose techniques". The key innovation? Noam Brown put it succinctly: "o1 thought for seconds. Deep Research for minutes. This one thinks for hours".

Again, it’s the same primary breakthrough: far extended thinking time. While this is a quantitative change, it may represent a fundamental shift in how we approach AI reasoning. It seems that rather than generating responses quickly, new models can engage in extended internal deliberation, exploring different approaches, backtracking when necessary, and building complex arguments over time. "Importantly, it's also more efficient with its thinking", Brown added, suggesting that the model has learned not just to think longer, but to think better.

This convergence on extended reasoning time as the key innovation is telling. Both teams independently discovered that mathematical insight often emerges not from clever algorithms or specialized architectures, but from giving models the space to explore, reconsider, and refine their thinking. This mirrors how many human mathematicians work—not in flashes of inspiration, but through patient exploration of the problem space.

What's particularly striking—and important going forward!—is that neither system relied heavily on formal methods. While AlphaProof had laboriously translated problems into Lean and searched for formal proofs, these new systems worked directly in natural language, producing arguments that human graders could evaluate using standard IMO criteria. This suggests that the path to mathematical AI might be more direct than previously thought—not through increasingly sophisticated formal systems, but through models that can engage with mathematics the way humans do.

It does look like OpenAI’s model is “more experimental” than Google’s Deep Think, though. It becomes clear when you look at the provided solutions. Here is Problem 1 from IMO 2025:

Here is a small sample of its solution by the OpenAI model:

Lemma: n>=4, any n-line cover of P_n must use a side of triangle.

Call boundary point set of triangle:

B_n = P_n ∩ (H_n ∪ V_n ∪ D_n): all integer points on 3 sides.

Count: each side has n lattice points. Three vertices each in two sides, no triple. So |B_n|= n+n+n -3=3n-3.

Now: L = {ℓ_1,…,ℓ_n} n distinct lines, cover all P_n. Suppose none of ℓ_i coincide with H_n,V_n,D_n.

Need contradiction for n>=4.

Geometry: T_n (filled triangle) is convex. Intersect any line ℓ with T_n:

ℓ∩T_n is empty / point / segment. If ℓ doesn’t contain whole side (that’s assumption), then ℓ∩∂T_n has at most two points (if segment, two endpoints). So: any line not equal to a side contains at most 2 points of boundary of T_n.

So each ℓ_i contains at most 2 points of B_n. So n lines cover at most 2n boundary points. But must cover all B_n (subset of P_n). Need 2n >= |B_n|=3n-3. For n>=4, 3n-3 >2n (difference n-3>0), impossible. Contradiction. So for n>=4, in any n-line cover of P_n, at least one of three side lines H_n, V_n, D_n is present. Exactly lemma. Good. (that’s main structural lemma)

So n>=4: any configuration has a boundary side line (non-sunny).

Now reduction from n to n-1.

Suppose n>=4, have n-line family L for P_n. Lemma gives side line E in L.

Remove E, get n-1 remaining lines.

Need show remaining (after appropriate translation) is configuration for P_{n-1}, same #sunny.

Three cases:

1) E = D_n: hyp line x+y=n+1. P_n \ D_n = {integer>=1 with sum<=n} = P_{n-1} exactly. D_n only hits sum=n+1 points, disjoint from P_{n-1}. So remaining n-1 lines alone cover P_{n-1}. Done, no transform.

2) E=H_n (y=1). Remaining points of P_n besides H_n: y>=2. Mapping down by 1 in y:

bijection T: (x,y+1) ↔ (x,y), between P_n \ H_n and P_{n-1}. Exactly: if (a,b) in P_{n-1}, (a,b+1) in P_n, y>=2, sum a+b+1<=n+1. Conversely. Take remaining n-1 lines ℓ in L{H_n}, translate downward by vector (0,-1). family L’ size n-1. For any p in P_{n-1}, p+(0,1) is in P_n \ H_n, covered by some ℓ; shift ℓ down, p covered by ℓ’. So L’ covers P_{n-1}. Translation preserves direction -> sunny status same.

3) E=V_n (x=1), same via shift (-1,0). Exactly same.

So any n-line cover for P_n (n>=4) -> n-1-line cover for P_{n-1}, same #sunny.

So iterate: for n>=4, reduce n -> n-1 -> … -> 3. Each step n>=4 (when parameter>=4) lemma applies. So any configuration for P_n (any n>=4) produces configuration for P_3 with same number of sunny lines. So possible k for n>=4 are subset of K_3. Great…

It is in English and is humanly understandable, but it’s a very special, very “professional” kind of English. Compare with a sampe from Deep Think’s solution of the same:

Importantly, Google waited for the IMO to officially certify the competition results rather than release its results over the weekend out of respect for the students in the competition. The solutions were evaluated by official IMO graders using the same standards applied to human contestants. As for OpenAI, for each problem three former IMO medalists independently graded the model’s submitted proof, with scores finalized after unanimous consensus.

Both systems struggled with Problem 6, highlighting that even gold-medal AI has limitations. The problem, which required a particularly creative insight, remained beyond current capabilities—a reminder that human mathematical intuition still has unique strengths.

And just for context, how long have AI researchers expected this? Alexander Wei, who led the OpenAI team solving IMO 2025, recalled the following: "In 2021, my PhD advisor, Jacob Steinhardt, had me forecast AI math progress by July 2025. I predicted 30% on the MATH benchmark... Instead, we have IMO gold".

We have another great datapoint about solving the IMO because back in 2022, prominent AI futurists placed their bets. Paul Christiano and Eliezer Yudkowsky discussed the “IMO grand challenge” as part of their takeoff speeds debate. Christiano wrote: "I'd put 4% on 'For the 2022, 2023, 2024, or 2025 IMO an AI built before the IMO is able to solve the single hardest problem'... Maybe I'll go 8% on 'gets gold'". Yudkowsky was more optimistic: "I'll stand by a >16% probability of the technical capability existing by the end of 2025". These predictions were made only three years ago, but now they seem to be hopelessly outraced by the actual speed of progress…

Of course, it was hard to predict all this in 2022, when GPT-3 had just been released. But here is a Manifold prediction market on this event. Note how the predicted probability jumps from about 50% to 96% after OpenAI’s announcement:

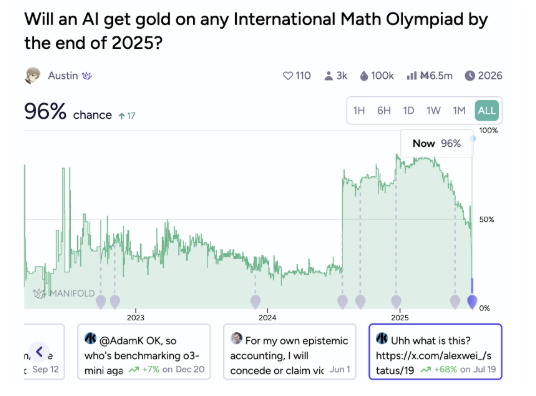
It was quite unexpected even in 2025!

Beyond the Medals: Implications for AI and Math Research

Gold medal performance by AI systems raises profound questions for mathematical education and research. If machines can solve IMO problems, what does this mean for how we teach mathematics and what we value in mathematical thinking?

On the one hand, AI tutors capable of IMO-level reasoning could revolutionize mathematics education. Imagine a personalized tutor that can:

• generate unlimited practice problems tailored to a student's level;
• provide step-by-step explanations in multiple ways until the student understands;
• identify conceptual gaps and address them systematically.

Yet there is a risk of demotivation. Why struggle with difficult problems when an AI can solve them instantly? The chess world provides an instructive parallel: despite (or perhaps because of) superhuman chess engines, human chess has flourished. The availability of perfect analysis tools has made human players stronger, not weaker. 

But chess is inherently a competition; we do not need to produce “the perfect chess game”, or even “the best possible analysis of a chess opening”, the point is to pit humans against each other. Math is different: we do genuinely care about proving new theorems, much more than about winning the IMO. And if you were looking for the objectively best chess game ever, for the last twenty years you wouldn’t go to humans.

For professional mathematicians, IMO-level AI might serve as a powerful research assistant. While IMO problems are relatively simple compared to research mathematics, the reasoning capabilities demonstrated suggest potential for: checking proofs for errors, exploring variations of theorems, generating conjectures based on known thinking patterns, and formalizing informal mathematical arguments.

Already, researchers are experimenting with these capabilities. At MIT, a team is using GPT-4 to generate and verify hundreds of variations of known theorems, searching for unexpected patterns. The Lean formalization project has accelerated dramatically, with AI assistants helping to translate entire textbooks into formal language. And at several universities, pilot programs are testing AI tutors that can provide IMO-level problem-solving guidance to advanced students.

The real test will come when these systems tackle open problems rather than well-posed competition questions. Can AI make genuine mathematical discoveries, or will it remain a sophisticated problem-solver? Only time will tell.

‍