LLMs have achieved remarkable capabilities through scale. But they remain fundamentally constrained by their shallow, fixed-depth architectures in complex reasoning tasks. In this post, we explore a recent very interesting idea that takes inspiration from the brain's hierarchical organization to create neural networks that can truly “think in layers”. It looks like the Hierarchical Reasoning Model (HRM) achieves state-of-the-art performance on challenging reasoning benchmarks with just 27M parameters, outperforming models thousands of times larger! Let’s discuss HRM's brain-inspired architecture and what it may mean for AI research.

The Current Bottleneck for Reasoning Models

Despite their remarkable success, today's large language models face a fundamental computational limitation: they're surprisingly shallow. While GPT-4 and Claude can write poetry and explain quantum mechanics, they struggle with tasks that require deep, multi-step reasoning—like solving hard Sudoku puzzles or finding optimal paths through complex mazes. 

A new paper from Sapient Intelligence, “Hierarchical Reasoning Model” (Wang et al., 2025), proposes an intriguing solution inspired by how the brain organizes computation across different timescales. Before we dive into their approach, let's understand why current models hit this wall.

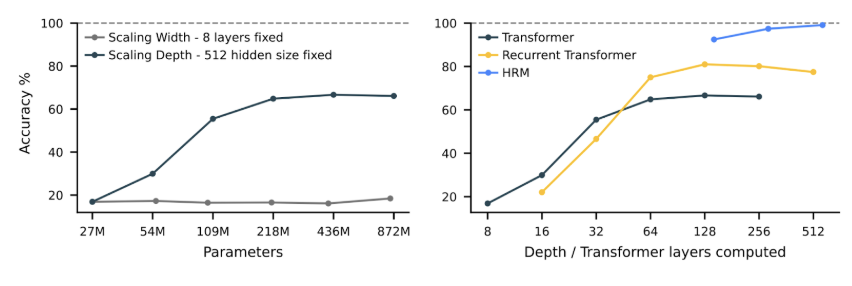
The answer lies in a constraint baked into the Transformer architecture itself: it has a fixed (and relatively small) number of layers. When you are activating billions of neurons per input, it actually means very wide parallel processing, but the number of sequential steps is usually in the dozens.

Since Transformers process information through a fixed number of layers, no matter how complex the problem, they get the same computational “depth” per forward pass. In theoretical computer science terms, they are stuck in constant-depth circuit classes (AC⁰ or TC⁰)—far from the polynomial-time algorithms needed for many reasoning tasks. Think of it like trying to solve a maze by looking at it for exactly 3 seconds, no matter how large or complex it is.

Reasoning models are a way around this limitation: they externalize the processing loop via intermediate tokens. And while current reasoning models are certainly impressive, it is essentially a hack with serious drawbacks:

• brittleness: one wrong intermediate step derails everything;
• data hunger: reasoning requires massive amounts of step-by-step training data;
• inefficiency: generates hundreds or thousands of tokens for complex problems;
• token-level constraints: forces reasoning through the bottleneck of natural language.

Recent attempts to improve CoT through reinforcement learning (Wang et al., 2025; Muennighoff, 2025) or curriculum training (Light-r1 by Wen et al., 2025) still operate within these fundamental constraints. What if, instead, we could let models reason in their hidden states—doing “latent reasoning” without the linguistic bottleneck?

Enter the Hierarchical Reasoning Model

The HRM takes inspiration from an unexpected source: the hierarchical organization of the brain. Neuroscience research shows that cortical areas operate at different timescales—fast sensory processing in lower areas, slower abstract reasoning in higher regions (Murray et al., 2014; Zeraati et al., 2023):

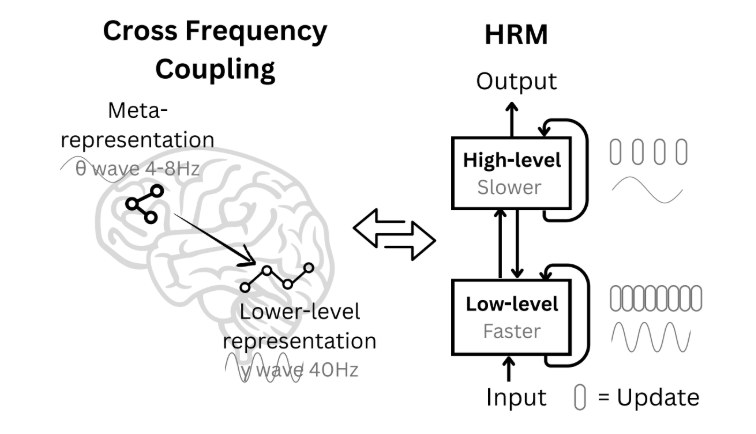
HRM implements this principle with two recurrent modules:

• a fast, low-level module that performs rapid, detailed computations;
• a slow, high-level module that provides abstract guidance and context.

During each forward pass, the low-level module runs for T steps while the high-level state remains fixed, converging toward a local solution. Then the high-level module updates based on what the low-level achieved, establishing a new context for the next cycle. This creates a hierarchy of nested computations—solving sub-problems within sub-problems.

The Technical Magic: Making It Work

The basic idea of nested RNNs is not that hard to come up with, but there are several technical issues that the authors had to overcome to make it work.

Solving the Convergence Problem. Standard recurrent networks face a serious problem: they converge too quickly, making later computational steps useless (the hidden state reaches a fixed point and stops changing meaningfully). HRM's hierarchical design cleverly sidesteps this through what the authors call “hierarchical convergence”:

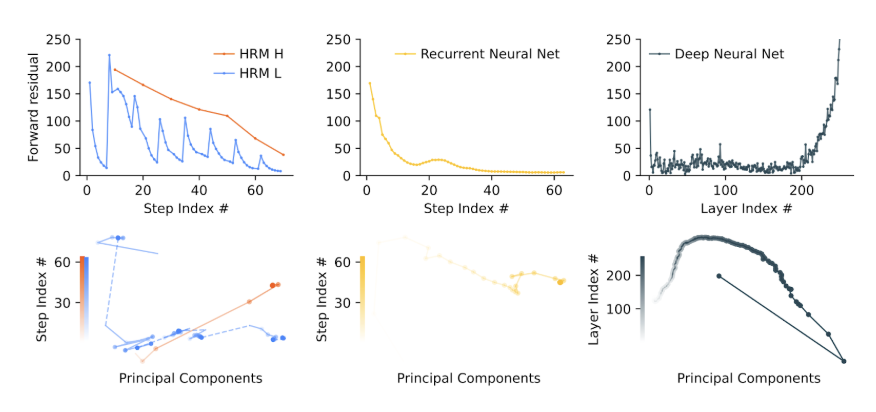
The low-level module converges within each cycle, but then gets "reset" when the high-level module updates, shifting the convergence target. It's like solving a series of related but distinct optimization problems rather than one that plateaus early.

Training Without Backpropagation Through Time. Here is where it gets really interesting. Training recurrent networks typically requires backpropagation through time (BPTT), which is memory-intensive and arguably biologically implausible. 

Instead, HRM borrows ideas from Deep Equilibrium Models (Bai et al., 2019) to compute gradients using only the final converged states: a “one-step gradient” that needs O(1) memory instead of O(T). In each training sample, only the latest step of the H-module and L-module are updated:

This connects to recent work on implicit models (Geng et al., 2021) and efficient training of recurrent architectures, but applies these ideas to a novel two-level hierarchical structure.

Adaptive Computation: Thinking Fast and Slow. Not all problems require the same amount of computation. HRM includes an adaptive halting mechanism trained via Q-learning, allowing it to “think longer” on harder problems. This builds on classic work like Adaptive Computation Time (Graves, 2016) and PonderNet (Banino et al., 2021), but with a simpler, more stable implementation. The results are quite impressive:

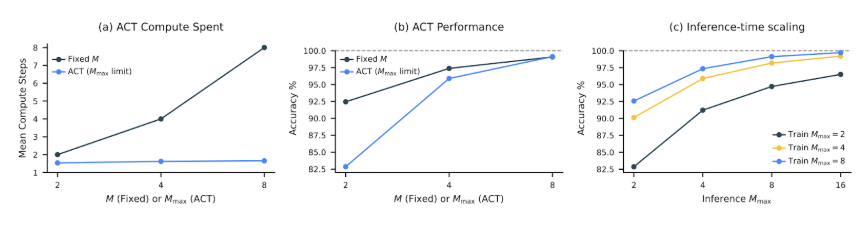
Experimental Proof: Exceptional Results with Minimal Data

Benchmarking. HRM really shines when it comes to the number of parameters. With just 27 million parameters and ~1000 training examples, it achieves:

• 40.3% on ARC-AGI-1 (vs. 34.5% for o3-mini-high and 21.2% for Claude);
• 55% exact solution rate on extremely hard Sudoku puzzles (where CoT models score 0%);
• 74.5% optimal path finding in 30×30 mazes (again, CoT models have a flat 0%).

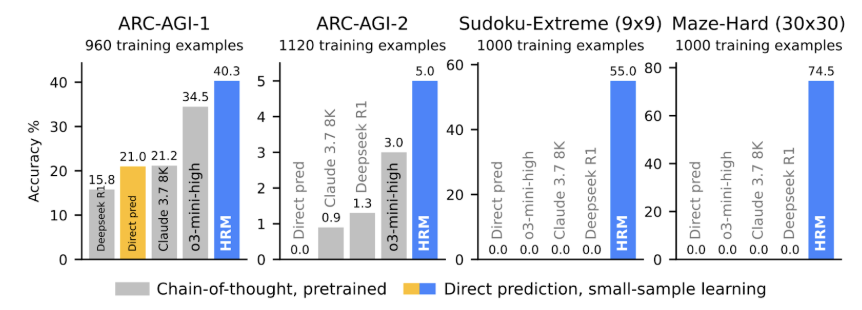
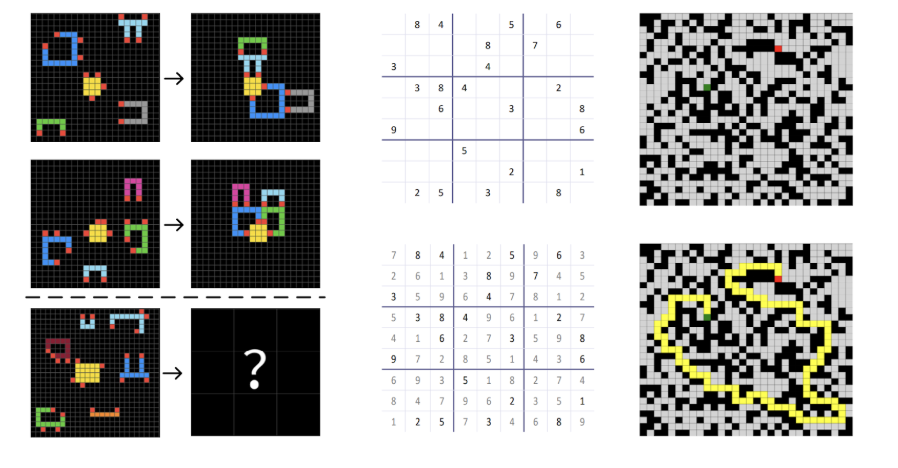
These are not cherry-picked easy problems. The Sudoku-Extreme dataset consists of puzzles averaging 22 backtracks in algorithmic solvers, far harder than standard benchmarks. The ARC tasks require abstract reasoning and rule induction from just 2-3 examples. Here are some sample problems, with ARC-AGI (left), Sudoku-Hard (center), and maze navigation (right):

Looking Inside: How Does It Actually Reason? The authors provide fascinating visualizations of intermediate states during problem-solving:

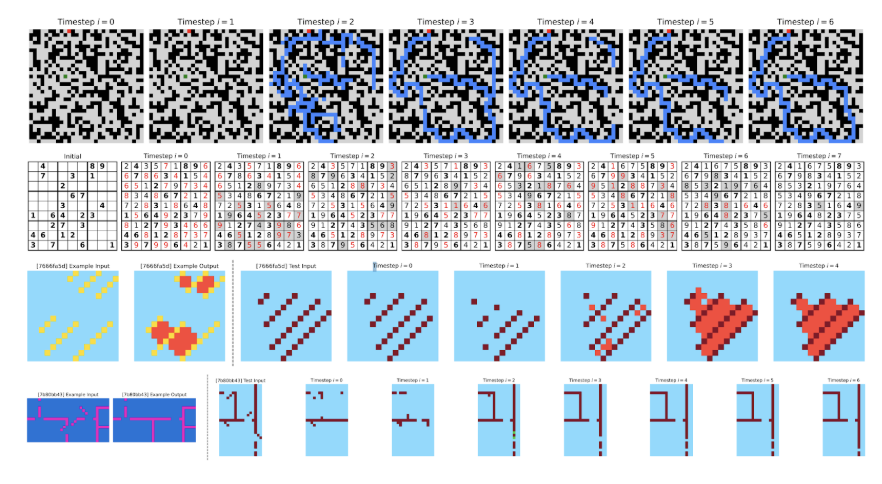
Here is what you can see there, top to bottom:

• in maze solving, HRM initially explores multiple paths, then prunes and refines;
• in sudoku puzzles, it exhibits depth-first search with backtracking—filling cells, detecting violations, and retracting;
• for ARC tasks, the traces look more like hill-climbing, making incremental adjustments.

This interpretability is also a crucial feature. Unlike CoT approaches where we see token-level steps, or black-box models where we see nothing, HRM offers a window into structured algorithmic reasoning.

The Brain Connection: Emergent Dimensionality Hierarchies

We started from a parallel to neuroscience that gave Wang et al. their core idea. But the parallel goes further! Trained HRM models spontaneously develop a “dimensionality hierarchy”, with the high-level module operating in a ~3x higher-dimensional representational space than the low-level module. This is very similar to the organization seen in biological neural networks (Posani et al., 2025):

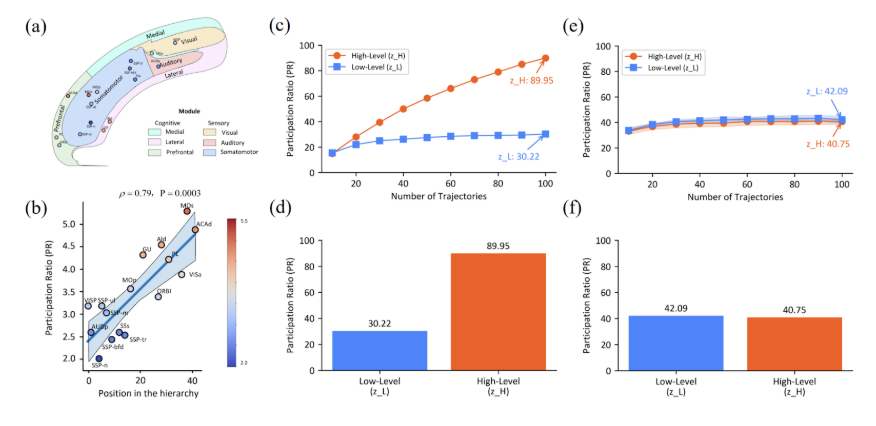
In this figure, (a) shows an anatomical illustration of mouse cortical areas and (b) shows the correlation between Participation Ratio (PR), a measure of effective dimensionality used in neuroscience, and position in the hierarchy. For the trained HRM, (c) shows how dimensionality scales with task diversity (“trajectories” mean unique tasks), and (d) illustrates that module H has much higher dimensionality than module L.

This was not built into the architecture—parts (e) and (f) of the figure above show that untrained networks do not show this pattern. It emerges from learning to solve complex reasoning tasks, suggesting the model has discovered a fundamental principle of hierarchical computation.

Context, Limitations, and Conclusion

The Hierarchical Reasoning Model sits at an interesting intersection of several research directions:

• neural algorithmic reasoners: models like Neural Turing Machines (Graves et al., 2014), Differentiable Neural Computers (Graves et al., 2016), and recent TransNAR (Bounsi et al., 2024) also aim to execute algorithms neurally; HRM is simpler architecturally but reports to have superior data efficiency through its hierarchical design;
• comparison with scaling approaches: while projects like Llama 3.1 (405B parameters) and GPT-4 bet on scale, HRM shows that architectural innovation can achieve strong reasoning with orders of magnitude fewer parameters; this aligns with recent work questioning pure scaling approaches (Villalobos et al., 2022);
• alternatives to recurrent models: recent linear attention methods and structured state-space models such as S4 and Mamba (Dao & Gu, 2024; Guo et al., 2025) offer different solutions to the quadratic complexity of attention; HRM is complementary, and it could potentially use these as building blocks while adding hierarchical structure;
• continuous thoughts: recent work on Continuous Thought Machines (Darlow et al., 2025) and latent reasoning (Chen et al., 2025; Shen et al., 2024) share HRM's goal of reasoning in continuous hidden states rather than discrete tokens, but take a different (and more straightforward) approach;
• alternative reasoning approaches: e.g., GOAT (Liu & Low, 2023) fine-tunes LLaMA specifically for arithmetic through careful data curation, search dynamics bootstrapping (Lehnert et al., 2024) uses A* search trajectories as training targets, while reasoning via energy diffusion (Du et al., 2024) frames reasoning as an iterative refinement process; HRM also provides an alternative path to reasoning, a very different one;
• brain-inspired AI architectures: the quest to replicate brain-like reasoning has a rich history; in recent work, let me highlight Spaun (Eliasmith et al., 2012) that uses spiking neural networks with modules corresponding to specific brain regions, the Tolman-Eichenbaum Machine (Whittington et al., 2020) which models hippocampal-entorhinal interactions for spatial and relational reasoning, and neural sampling models (Buesing et al., 2011) that view neural computation as probabilistic inference.

However, let us also be clear about what HRM has not shown:

• all evaluations are on structured grid puzzles, not natural language reasoning or real-world planning;
• the ARC results rely heavily on test-time augmentation (1000 variants);
• "near-perfect" sudoku performance requires the full 3.8M training set, not just 1000 examples.

Finally, the most fundamental remaining question is this: can these ideas scale to LLM-sized parameters and datasets? If yes, it could be an honest to God breakthrough.

In conclusion, HRM represents a fascinating alternative to the dominant paradigm of scaling LLMs and augmenting them with reasoning. By taking inspiration from neuroscience and combining it with modern deep learning techniques (equilibrium models and adaptive computation), it achieves remarkable reasoning capabilities with minimal resources.

The key insights of Wang et al. (2025)—hierarchical timescale separation, convergence management through periodic resets, and emergence of dimensionality hierarchies—may prove valuable even beyond this specific architecture. As AI research pushes toward more capable reasoning systems, HRM represents a fascinating alternative to scaling. Perhaps sometimes the path forward is not through more parameters or more tokens, but through fundamentally rethinking how neural networks perform computation.

Whether HRM's approach will scale to the full complexity of human-like reasoning remains to be seen. But in a field increasingly dominated by brute-force scaling, it is refreshing to see that clever architecture design still has surprises to offer.

‍